Subsection 1.1.9 Differentiation of a Vector with respect to Scalars
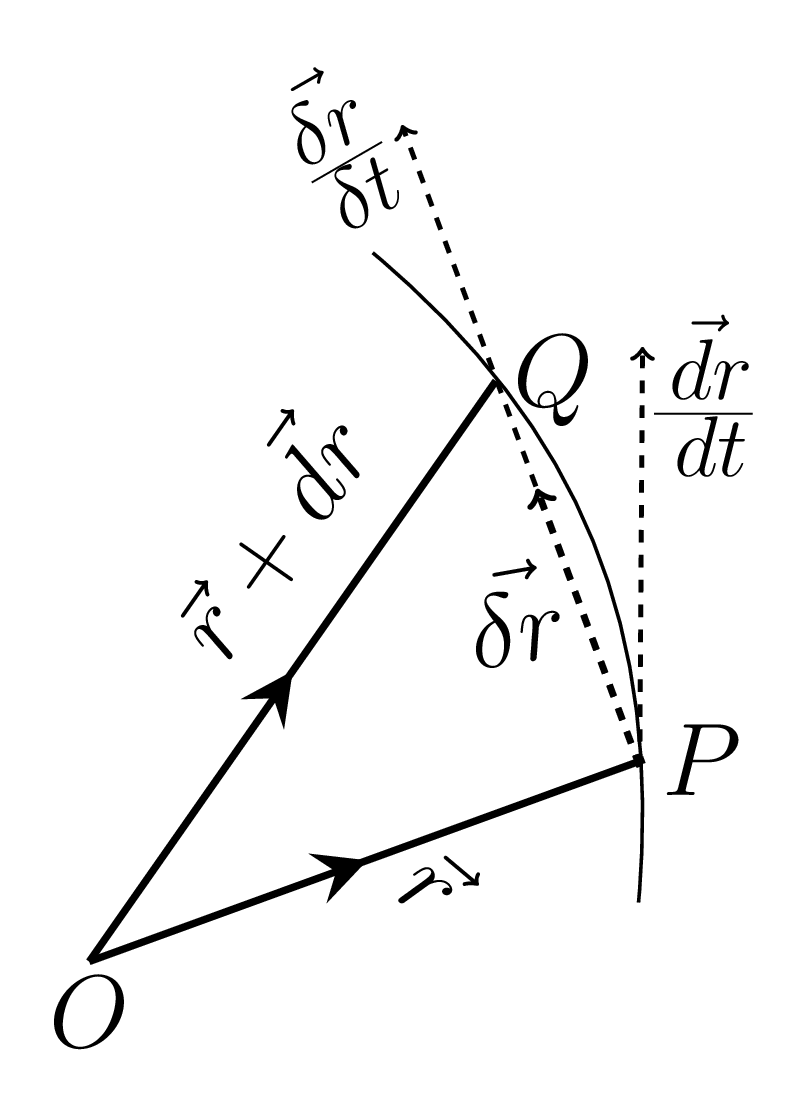
Let the vector \(\vec{r}\) be a function of scalar variable \(t\text{,}\) then \(\vec{r} = \vec{f\left(t\right)}\text{.}\) If only one value of \(\vec{r}\) corresponds to each value of \(t\text{,}\) then \(\vec{r}\) is defined as a single valued function of the scalar variable \(t\text{.}\) If \(t\) varies continuously with \(\vec{r}\text{,}\) then the end point of \(\vec{r}\) describes a continuous curve. For different values of \(t\text{,}\) the end point of the vector describes the curve, as shown in figure Figure 1.1.11 and can be expressed as the following vector equations.
\begin{align*}
\vec{r} \amp = a \cos t\hat{i} + a \sin t\hat{j} \quad \text{(circle)}; \\
\vec{r}\amp = a \cos t\hat{i} + b \sin t\hat{j} \quad \text{(ellipse)}; \\
\vec{r} \amp = a t^{2}\hat{i} + 2 a t\hat{j} \quad \text{(parabola)};\quad \text{and}\\
\vec{r} \amp = a \sec t\hat{i} + b \tan t\hat{j} \quad \text{(hyperbola)}.
\end{align*}
Note: Any vector \(f(t)\) can also be written in the form \(\vec{f}\left(t\right) = f_{1}\left(t\right)\hat{i} + f_{2}\left(t\right)\hat{j}
+ f_{3}\left(t\right)\hat{k}\) where \({f_{1}\left(t\right)}\text{,}\) \({f_{2}\left(t\right)}\text{,}\) \({f_{3}\left(t\right)}\) are three scalar functions of \(t\text{.}\) Now, Let O be the origin and P be the position of a moving particle at time \(t\text{,}\) as shown in figure Figure 1.1.11. After the interval \(t+\delta t\) the particle reaches at Q, so that
\begin{equation*}
\vec{PQ} = \vec{OQ} - \vec{OP} = \vec{r}+\vec{\delta r} - \vec{r} = \vec{\delta r}
\end{equation*}
[\(\because \vec{OQ} = \vec{r}+\vec{\delta r}\) and \(\vec{OP} = \vec{r}\text{,}\) the position vectors.] Since, \(\vec{PQ}\) subtands in time \(\delta t\text{,}\) hence in unit time the vector will be \(\vec{PQ}/\delta t\text{,}\) or, \(\vec{\delta r}/\delta t\text{.}\) As \(\delta t \to 0\text{,}\) point Q tends to point P and the chord becomes the tangent at P, we define
\begin{equation*}
\frac{\vec{\,dr}}{\,dt} = \lim\limits_{\,\delta t \to 0} \frac{\vec{\,\delta r}}{\,\delta t}
\end{equation*}
Then, \(\frac{\vec{d r}}{d t}\) is a vector in the direction of tangent at P and defines the velocity of the particle at P, \(\frac{\vec{\,dr}}{\,dt}\) is also called the differential coefficient of \(\vec{r}\) with respect to ’t’. Similarly, \(\frac{ {\,d^{2} \vec{r}}}{\,dt^{2}}\) is the second order derivative of \(\vec{r}\) which gives the acceleration of the particle at P. Note: The derivative of a constant vector \(\vec{C}\) is zero, i.e. if \(\vec{C}\) is a constant vector, then \(\frac{\vec{\,dC}}{\,dt} = 0\text{,}\) because there is no change in \(\vec{C}\) in the interval \(\delta t\text{.}\)
