Chapter 1 Vector Analysis
In order to describe a physical world we need a variety of physical quantities. Any physical property which can be quantitized and measured in numbers is called a physical quantity. The property such as ’anger, happiness, feelings, emotion, etc. can not be quantitized and measured, hence they are not taken as physical quantities. There are two types of physical quantities usually consider to describe a physical world. They are a scalar quantity (or, simply scalars) and a vector quantity (or, simply vectors) A scalar quantity has only magnitude (size) e.g., mass, length, time, volume, density, work, speed, temperature, potential, current, resistance, flux, power, intensity, etc. A vector quantity has both magnitude and direction e.g., velocity, acceleration, displacement, momentum, force, torque, impulse, moment, current density, etc. A quantity like surface area is a scalar in general, but when considered with its specific orientation it is taken as a vector. In physics, area is a vector quantity whose direction is always taken as an outward normal to the surface. Normally, when area comes with any vectors in a mathematical operation it is considered as a vector. For instance, flux is a dot product of two vectors, one of them is an area. Mathematically, division of a vector with another vector is undefined, hence pressure is considered as a scalar even if it is defined as a force per unit area. To define pressure in general as a scalar we divide a magnitude of the normal component of the force to the magnitude of the area. Actually, pressure has more than one direction, hence it is a complex quantity which comes under tensors. The concept of tensors are not made known in elementary courses. A tensor is a vector generalization of physical quantities. (We will discuss tensors later in this book.)
A vector is represented by an arrow. The arrow shows the direction of a vector and the length of the arrow represents the magnitude of that vector. Points \(O\) and \(P\) of an arrow \(OP\) in Figure 1.0.1.(a) are known as the initial point and the terminal point of the vector \(\textbf{OP}\text{,}\) respectively. A vector is denoted by a letter with an arrow over it such as \(\vec{OP} = \vec{a}\) and its magnitude is denoted by \(\vec{|a|}\) or simply by \(a\text{.}\) A vector of unit magnitude is called a unit vector and is denoted by \(\hat{a}\text{,}\) (’a cap’), Where \(\hat{a}=\frac{\vec{a}}{\vec{|a|}}\text{,}\) i.e., \(\hat{a}\) is a unit vector of \(\vec{a}\text{.}\)
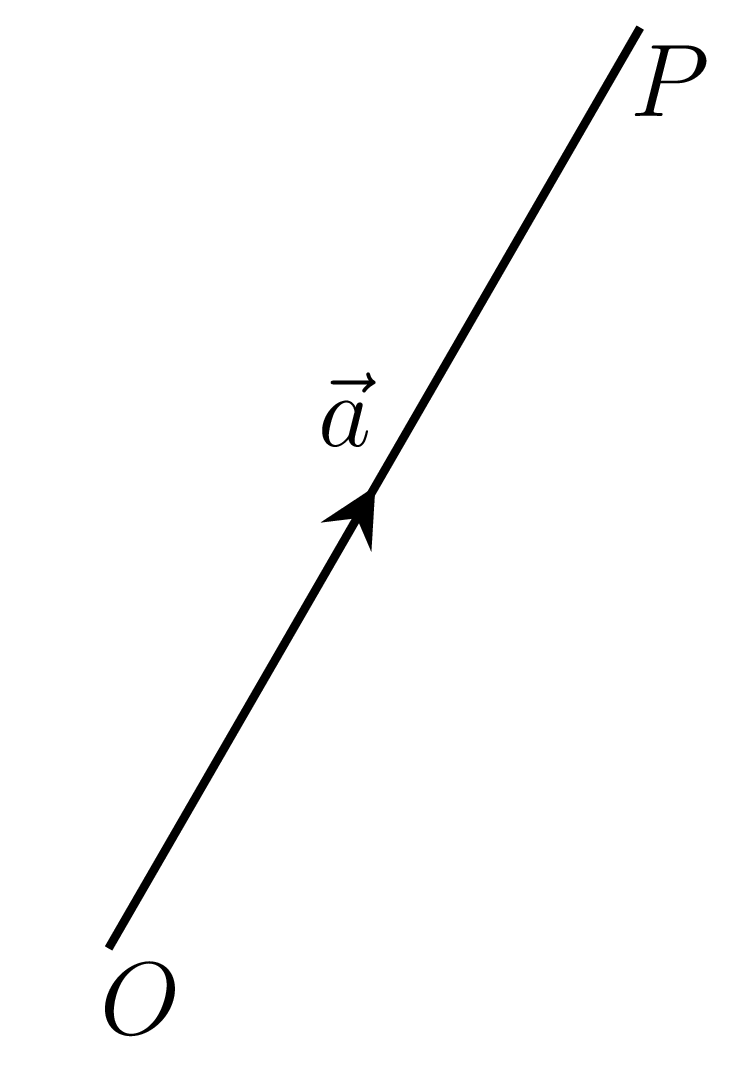
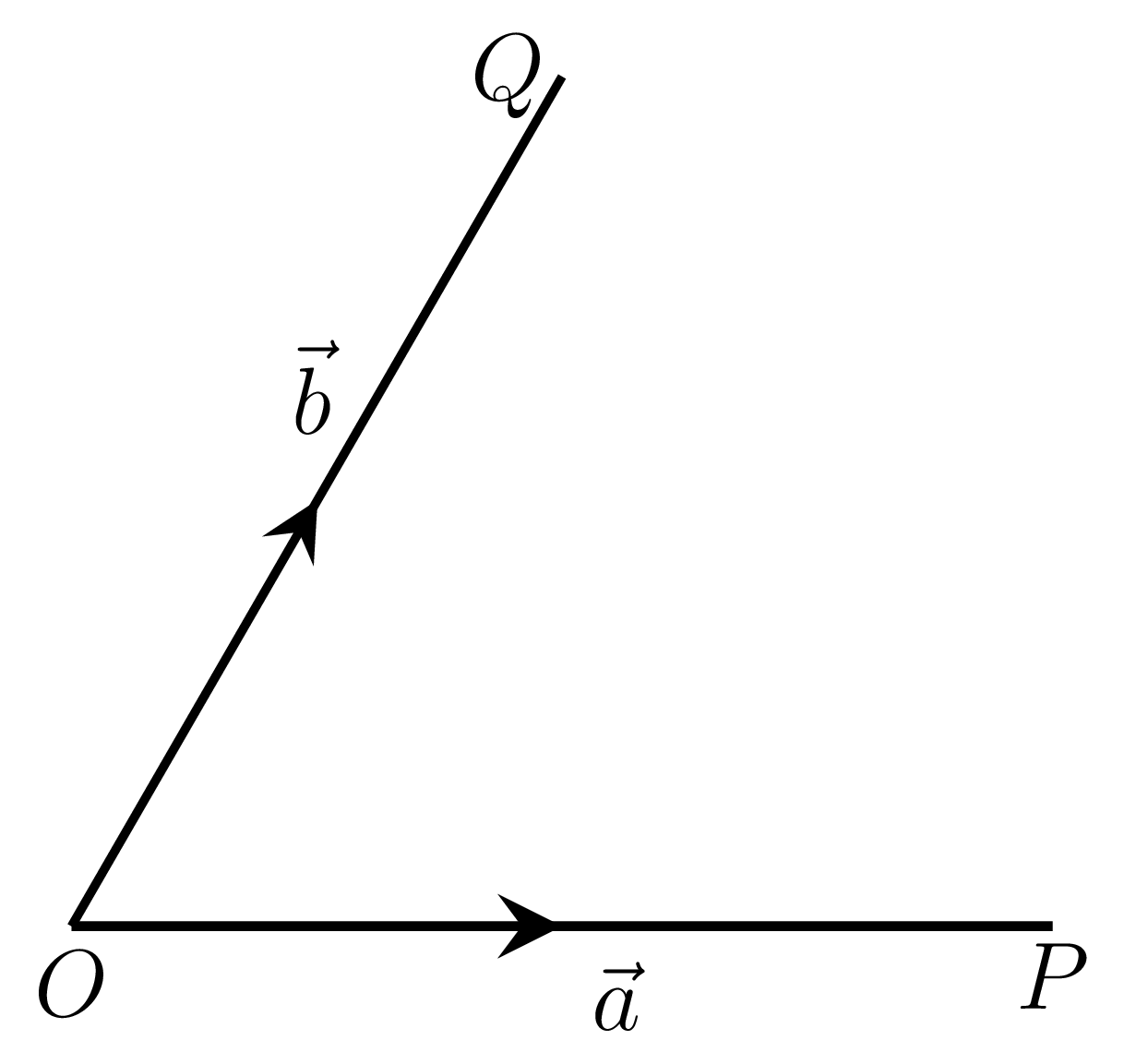
A vector which specifies the position of point P with respect to its origin O is called a position vector, as shown in Figure 1.0.1.(a). Let P and Q be two points and O be the point of origin then the position vector of point P is \(\vec{OP}\) and that of point Q is \(\vec{OQ}\text{,}\) as shown in Figure 1.0.1.(b). A vector of zero magnitude is a null vector. It is denoted by \(\vec{O}\text{.}\) The initial and terminal points coincide in case of a null vector. Thus it has no definite direction. The vectors with same magnitude but in opposite direction are termed as negative vectors. Vectors having the same direction are called like vectors, whereas those having opposite directions are called unlike vectors. The vectors parallel to the same line regardless of their magnitudes and directions are called collinear vectors. In this case, there exists a scalar \(\lambda \) such that \(\vec{b} =\lambda \vec{a}\) in the collinear vectors \(\vec{a}\) and \(\vec{b}\text{.}\) The vectors whose directions are not parallel to each other are non-collinear vectors. A system of vectors lying in the parallel planes or in the same plane are called coplanar vectors. The system of vectors which can not lie in the same plane or parallel planes are called non-coplanar vectors.
