Section 7.1 One Dimensional Wave Equation in Stretched String
Let us consider an elastic string tightly stretched between points O and P by constant tension T. The string is caused to vibrate by plucking it with a very small displacement ’y’ at time ’t’ so that the tension T remains constant throught the deflections of the string. Let \(m\) be the mass per unit length of an element AB of the vibrating string, as shown in figure Figure 7.1.1. The net force acting on the element AB in x and y directions is given by
\begin{equation}
F_{x}=T\cos \beta -T \cos \alpha\tag{7.1.1}
\end{equation}
and
\begin{equation}
F_{y}=T\sin \beta -T \sin \alpha\tag{7.1.2}
\end{equation}
where \(\alpha\) and \(\beta\) are the inclination of tension T with the horizontal x - axis.
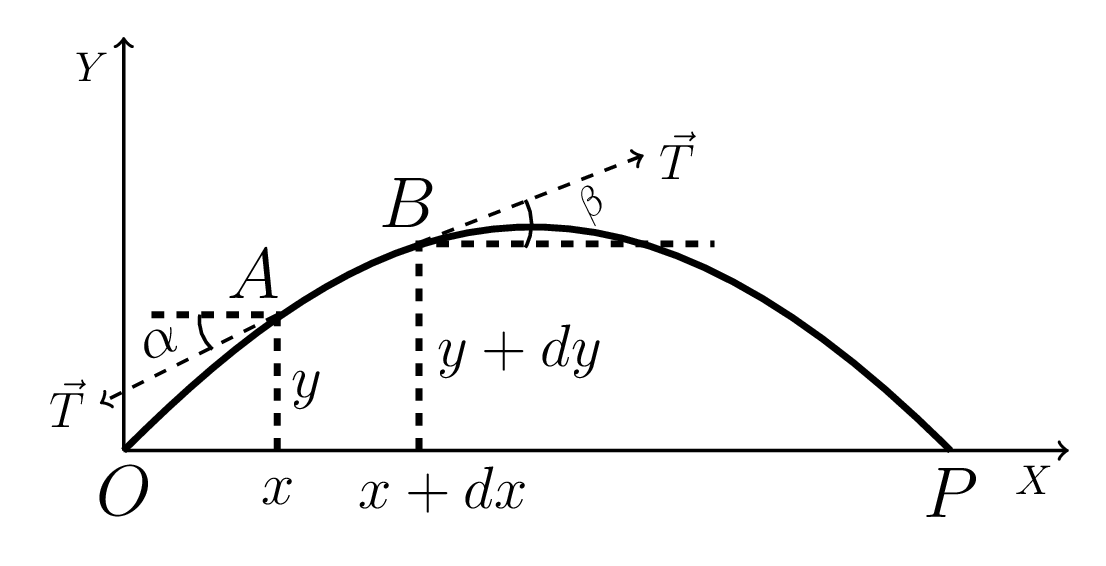
For small displacement
\begin{equation*}
\cos\beta = \cos \alpha \Rightarrow F_{x} =0,
\end{equation*}
i.e., the motion of the particle of string along x - axis is zero. Also,
\begin{equation*}
\sin\beta = \tan\beta = \left(\frac{\partial y}{\partial x}\right)_{B} = \left(\frac{\partial y}{\partial x}\right)_{x+\,dx}
\end{equation*}
and
\begin{equation*}
\sin\alpha = \tan\alpha = \left(\frac{\partial y}{\partial x}\right)_{A} = \left(\frac{\partial y}{\partial x}\right)_{x}
\end{equation*}
where \(\frac{\partial y}{\partial x}\) defines the slope of tangents at a perticular point at any time ’t’. From equation (7.1.2), we have -
\begin{equation*}
F_{y}=T\left(\frac{\partial y}{\partial x}\right)_{x+\,dx}-T\left(\frac{\partial y}{\partial x}\right)_{x}
\end{equation*}
\begin{equation*}
=T\left[\left(\frac{\partial y}{\partial x}\right)_{x+\,dx}-\left(\frac{\partial y}{\partial x}\right)_{x}\right]
\end{equation*}
\begin{equation*}
=T\left[\left(\frac{\partial y}{\partial x}\right)_{x}+\frac{\partial}{\partial x}\left(\frac{\partial y}{\partial x}\right)_{x}\,dx+\cdots-\left(\frac{\partial y}{\partial x}\right)_{x}\right]
\end{equation*}
(using Taylor’s expansions)
\begin{equation}
\therefore F_{y}=T\frac{\partial^{2} y}{\partial x^{2}}\,dx\tag{7.1.3}
\end{equation}
(neglicting higher order terms.) i.e., \(F_{y} \neq 0\) hence the motion of the particle of string is only along y - axis.
If the acceleration of the element along vertical be \(\frac{\partial^{2} y}{\partial t^{2}}\) and mass of an element AB is \(m\,ds\) then according to Newton’s second law of motion, this force is given by
\begin{equation}
F_{y} = m\,ds\frac{\partial^{2} y}{\partial t^{2}}\tag{7.1.4}
\end{equation}
\begin{equation*}
T\frac{\partial^{2} y}{\partial x^{2}}\,dx = m\,dx\frac{\partial^{2} y}{\partial t^{2}}
\end{equation*}
[Since, slope of the curve is small, \(\,ds\) can be replaced by \(\,dx\text{.}\)]
\begin{equation*}
T\frac{\partial^{2} y}{\partial x^{2}} = m\frac{\partial^{2} y}{\partial t^{2}}
\end{equation*}
or,
\begin{equation}
\frac{\partial^{2} y}{\partial x^{2}} = \frac{1}{v^{2}}\frac{\partial^{2} y}{\partial t^{2}}\tag{7.1.5}
\end{equation}
It is the wave equation for a vibrating string, where \(v^{2}=\frac{T}{m}\) is the velocity of the wave propagating along the string.
