Subsection 1.6.6 Spherical Orthogonal Curvilinear Coordinates
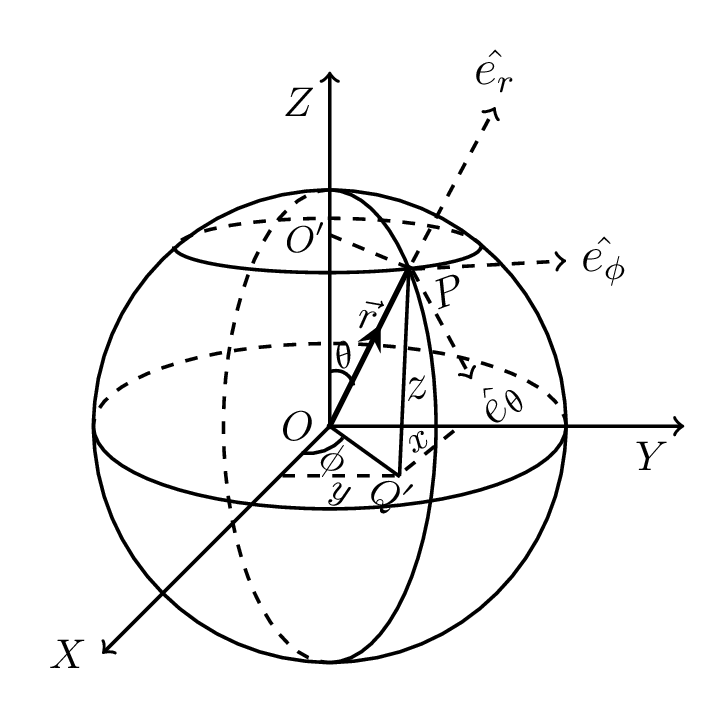
Let \((u,v,w)\) be the curvilinear coordinates of point P and \((x,y,z)\) be its corresponding cartesian coordinates. If \(\vec{r}\) be the position vector of point P then the spherical coordinates of point P are specified by \((r, \theta, \phi)\text{,}\) as shown in Figure 1.6.3. where \(r\geq 0, \quad 0\leq \theta \leq \pi, \quad 0\leq \phi \leq 2\pi\text{.}\) The corresponding transformation into cartesian systems are \(x=OQ\cos\phi = O'P\cos\phi = r\sin\theta \cos\phi\text{,}\) \(y=OQ\sin\phi = r\sin\theta \sin\phi\text{,}\) and \(z=PQ= OO'= OP\cos\theta = r\cos\theta\text{.}\) Here,
\begin{equation*}
x=x(r{,}\theta{,}\phi)
\end{equation*}
or,
\begin{equation*}
\,dx= \frac{\partial x}{\partial r}\,dr +\frac{\partial x}{\partial \theta}\,d\theta
+ \frac{\partial x}{\partial \phi}d\phi
\end{equation*}
\begin{equation*}
= \sin\theta\cos\phi \,dr+ r\cos\theta\cos\phi \,d\theta-r\sin\theta \sin\phi \,d\phi
\end{equation*}
Similarly,
\begin{equation*}
\,dy= \sin\theta\sin\phi \,dr+ r\cos\theta\sin\phi \,d\theta +r\sin\theta \cos\phi \,d\phi
\end{equation*}
and
\begin{equation*}
\,dz= \cos\theta \,dr+ -r\sin\theta \,d\theta.
\end{equation*}
\begin{equation*}
\therefore \quad \,ds^{2}= dx^{2}+dy^{2}+\,dz^{2}
\end{equation*}
\begin{equation}
= \,dr^{2}+r^{2}\,d\theta^{2}+r^{2}\sin^{2}\phi \,d\phi^{2}\tag{1.6.15}
\end{equation}
But in curvilinear coordinates
\begin{equation*}
\,ds^{2}= h_{1}^{2} \,du^{2}+h_{2}^{2} \,dv^{2}+h_{3}^{2} \,dw^{2}
\end{equation*}
\begin{equation*}
h_{1} = 1,\quad h_{2}=r, \quad h_{3}=r\sin\theta,
\end{equation*}
and (u,v,w) is replaced by \((r, \theta, \phi)\text{,}\) and \(\hat{e}_{1} = \hat{e}_{r}{,}
\hat{e}_{2}=\hat{e}_{\theta}{,}
\hat{e}_{3} =\hat{e}_{\phi}\text{.}\)
Alternative method to find \(h_{1},h_{2},h_{3}\) The position vector of point P in spherical coordinates is
\begin{equation*}
\vec{r}= x\hat{i}+y\hat{j}+z\hat{k}
= r\sin\theta \cos\phi\hat{i}+r\sin\theta \sin\phi\hat{j}+r\cos\theta\hat{k}
\end{equation*}
The tangent vectors of which is given as
\begin{equation*}
\frac{\partial\vec{r}}{\partial r}
=\sin\theta \cos\phi\hat{i}+\sin\theta \sin\phi\hat{j}+\cos\theta\hat{k} \quad
\Rightarrow h_{1}=\mid\frac{\partial\vec{r}}{\partial r}\mid =1.
\end{equation*}
\begin{equation*}
\frac{\partial\vec{r}}{\partial \theta}
=r\cos\theta \cos\phi\hat{i}+r\cos\theta \sin\phi\hat{j}-r\sin\theta\hat{k}\quad
\Rightarrow h_{2}=\mid\frac{\partial\vec{r}}{\partial \theta}\mid =r;
\end{equation*}
\begin{equation*}
\frac{\partial\vec{r}}{\partial \phi}
= -r\sin\theta \sin\phi\hat{i}+r\sin\theta \cos\phi\hat{j} \quad
\Rightarrow h_{3}=\mid\frac{\partial\vec{r}}{\partial \phi}\mid =r\sin\theta.
\end{equation*}
Now, substituting these values in different expressions in curvilinear system, we get -
\begin{equation*}
\vec{\nabla\psi}=\frac{\partial \psi}{\partial r}\hat{e_{r}}
+\frac{1}{r}\frac{\partial \psi}{\partial \theta}\hat{e_{\theta}}
+\frac{1}{r\sin\theta}\frac{\partial \psi}{\partial \phi}\hat{e_{\phi}};
\end{equation*}
\begin{equation*}
\vec{\nabla}\cdot\vec{F}=\frac{1}{r^{2}}\frac{\partial}{\partial r}(r^{2}F_{1})
+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta F_{2})
+\frac{1}{r\sin\theta}\frac{\partial F_{3}}{\partial \phi}
\end{equation*}
\begin{equation*}
\vec{\nabla}\times\vec{F} = \frac{1}{r\sin^{2}\theta}{\begin{vmatrix}
\hat{e}_{r} & r\hat{e}_{\theta} & r\sin\theta\hat{e}_{\phi} \\
\frac{\partial}{\partial r} & \frac{\partial}{\partial \theta} & \frac{\partial}{\partial \phi} \\
F_{1} & r F_{2} & r\sin\theta F_{3}
\end{vmatrix}};
\end{equation*}
\begin{equation*}
\nabla^{2}\psi
= \frac{1}{r^{2}\sin\theta} \left[\sin\theta\frac{\partial}{\partial r}\left(r^{2}\frac{\partial \psi}{\partial r}\right)
+\frac{\partial}{\partial \theta}\left(\sin\theta \frac{\partial \psi}{\partial \theta}\right)
+\frac{1}{\sin\theta}\frac{\partial^{2}\psi}{\partial \phi^{2}}\right]
\end{equation*}
\begin{equation*}
=\frac{1}{r^{2}}\frac{\partial}{\partial r}\left(r^{2}\frac{\partial \psi}{\partial r}\right)+
\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial \theta}\right)
\end{equation*}
\begin{equation*}
+ \frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2}\psi}{\partial \phi^{2}}
\end{equation*}
\begin{equation*}
=\frac{\partial^{2} \psi}{\partial r^{2}}
+\frac{1}{r^{2}}\frac{\partial^{2} \psi}{\partial \theta^{2}}
+\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2}\psi}{\partial \phi^{2}}
\end{equation*}
\begin{equation*}
+\frac{2}{r}\frac{\partial \psi}{\partial r}
+\frac{\cot\theta}{r^{2}}\frac{\partial \psi}{\partial \theta}.
\end{equation*}
