Subsection 1.2.2 Divergence of a Vector Function
If \(\vec{F}=F_{1}\hat{i}+F_{2}\hat{j}+F_{3}\hat{k}\) be the vector point function then divergence of a vector is defined as
\begin{equation*}
\,div \vec{F} = \vec{\nabla}\cdot\vec{F}
\end{equation*}
\begin{equation*}
= \left(\hat{i}\frac{\partial }{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z}\right)\cdot \left(F_{1}\hat{i}+F_{2}\hat{j}+F_{3}\hat{k}\right)
\end{equation*}
\begin{equation*}
=\left(\frac{\partial F_{1} }{\partial x}+\frac{\partial F_{2}}{\partial y}+\frac{\partial F_{3}}{\partial z}\right).
\end{equation*}
which is a scalar quantity.
Subsubsection 1.2.2.1 Physical Significance of \(\vec{\bigtriangledown}\cdot\vec{F}\)
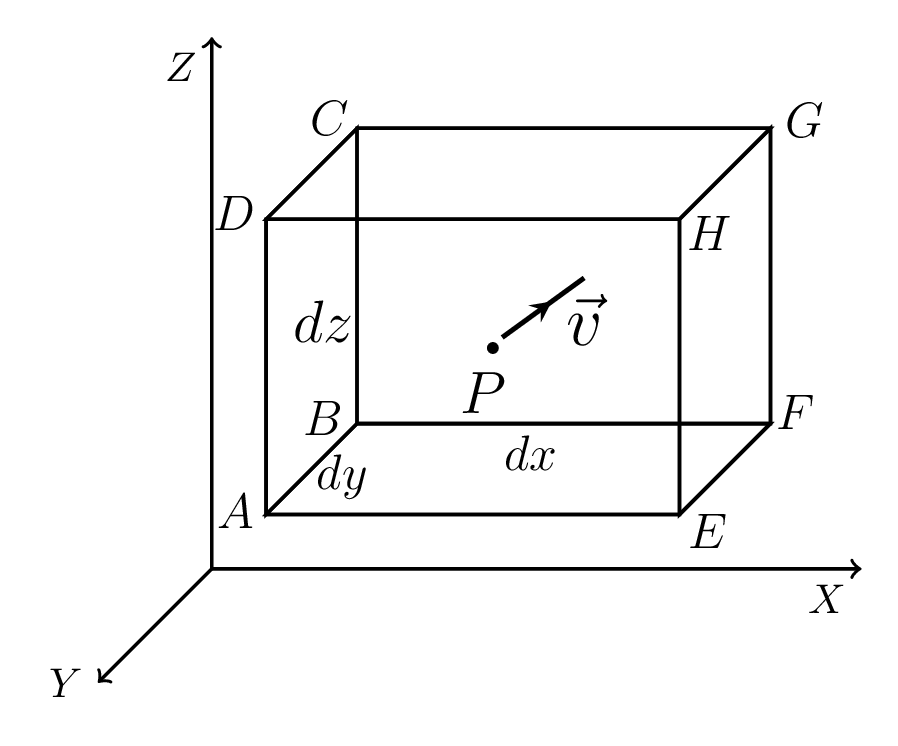
Let \(\vec{v}=v_{1}\hat{i}+v_{2}\hat{j}+v_{3}\hat{k}\) be the velocity of fluid at point P \((x,y,z)\text{.}\) If P be the centre of an elementary parallelopiped considering in the moving fluid and \(\,dx, \,dy, \,dz\) are the edges of such element, then the x- component of velocity at point P = \(v_{x} (x,y,z)\text{,}\) as shown in figure. The x- component of velocity at the middle of the face ABCD = \(v_{x} (x-\frac{\,dx}{2},y,z)\)
\begin{equation*}
= v_{x} (x,y,z)-\frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx
\end{equation*}
[using Taylor’s series, \(f(x+\,dx) = f(x)+f'(x)\,dx+ f"(x)/2 (\,dx)^{2} +\cdots \)]
Similarly, x- component of velocity at the middle of face EFGH
\begin{equation*}
=v_{x} (x+\frac{\,dx}{2},y,z)
= v_{x}(x,y,z) + \frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx.
\end{equation*}
Since the parallelopiped is very small, the value at the middle of face is considered as the average over that face. The volume of fluid entering per unit time through the face ABCD =velocity \(\times\) area of the face
\begin{equation*}
=\left( v_{x} - \frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx\right) \,dy \,dz
\end{equation*}
\begin{equation*}
[\because \frac{volume}{time} = \frac{area\cdot length}{time} = velocity\cdot area]
\end{equation*}
and volume of fluid leaving per unit time through face EFGH
\begin{equation*}
=\left( v_{x} + \frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx\right) \,dy \,dz.
\end{equation*}
Therefore, loss in volume of fluid per unit time along x- axis
\begin{equation*}
=\left( v_{x} + \frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx\right) \,dy \,dz - \left(v_{x} - \frac{1}{2}\frac{\partial v_{x}}{\partial x} \,dx\right) \,dy \,dz
\end{equation*}
\begin{equation*}
= \frac{\partial v_{x}}{\partial x} \,dx \,dy \,dz
\end{equation*}
Similarly, losses in volume per unit time along y- and z- axes, respectively are
\begin{equation*}
\frac{\partial v_{y}}{\partial y}dx dy dz \hspace{5pt}\text{and} \hspace{5pt} \frac{\partial v_{z}}{\partial z}\,dx \,dy \,dz.
\end{equation*}
Hence, total loss in volume per unit time = \(\frac{\,dV}{\,dt}\)
\begin{equation*}
= \left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}+\frac{\partial v_{z}}{\partial z}\right)\,dx \,dy \,dz
\end{equation*}
or, total loss in volume per unit time per unit volume = \(\frac{1}{\,dV}\frac{\,dV}{\,dt}\)
\begin{equation*}
=\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}+\frac{\partial v_{z}}{\partial z}\right)
\end{equation*}
\begin{equation*}
=\left(\hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z}\right)\cdot \left(v_{x}\hat{i}+v_{y}\hat{j}+v_{z}\hat{k}\right)
\end{equation*}
\begin{equation*}
= \vec{\nabla}\cdot\vec{v} = div \vec{v}
\end{equation*}
The divergence of a vector field at a point gives the rate at which the fluid is diverging from that point per unit volume. If div \(\vec{v}\) is positive at a point, then either the fluid is expanding and its density at that point is decreasing with time, or the point is a source of the fluid. If div \(\vec{v}\) is negative, then either the fluid is condensing and its density is increasing at that point, or the point is a sink. If the fluid is incompressible, then there is no loss or gain in volume.
Hence, div \(\vec{v} =0\text{,}\) and \(\vec{v}\) is called a solenoidal vector function.
