Subsection 2.1.1 Equations of Motion
There are three equations of motion defined by the above terminologies which can help solve problems of motion. These eqations are obtained by manipulating average velocity and acceleration of the object.
-
Equations of motion in horizontal direction: Section 2.3
- \(v_{f}=v_{i}+at\text{.}\)
- \(v^2_{f}=v^2_{i}+2ad\text{.}\)
- \(d=v_{i}t+\frac{1}{2}at^2\text{.}\)
-
Equations of motion in vertical direction: Section 2.3
- \(v_{f}=v_{i}+gt\text{.}\)
- \(v^2_{f}=v^2_{i}+2gh\text{.}\)
- \(h=v_{i}t+\frac{1}{2}gt^2\text{.}\)
Here, \(g\) = acceleration due to gracvity, \(h\) = height attains by the object, and \(t\) = time taken by the object during its motion.
In vertical direction earth plays a vitol role in the acceleration of object motion. Earth pulls every thing downwards which causes acceleration due to gravity, \(g\) negative. Accleration due to gravity is the acceleration of the object caused by the earth gravitational field. The value of \(g =9.8 m/s^2\text{.}\) In vertical motion, we consider height as positive if going up (y-axis) and height as negative if coming down. But here, we are taking \(g = -9.8 m/s^2.\) if the object is going vertically up, and \(g =+9.8 m/s^2.\) for the object falling down. Such conventions allow us to assume h as always positive.
Note: The above equations only work for constant acceleration or acceleration due to gravity.
Subsubsection 2.1.1.1 Free Fall
Objects moving under the influence of only gravity is called a free fall, . This means gravity causes a change in the velocity of any object by 9.80 \(m/s\) every second. So, drop any object and let it fall toward the ground: After 1s, the speed of the object is 9.80 \(m/s\text{.}\) After 2s, the speed of the object is 19.6 \(m/s\text{,}\) etc. According to Galileo the velocity of a falling object is proportional to the length of time that the object has been falling. From the first equation of motion
\begin{align*}
v_f-v_i \amp =gt\\
\text{or,} \quad v \amp =gt, \\
\quad \therefore v \amp \propto t,
\end{align*}
as \(g\) is a constant. Hence, the object is falling with higher velocity if it is falling for a long time or from a higher position. Since \(g\) is constant near the planet all objects fall at the same rate. (Assuming there is no air resistance).
Subsubsection 2.1.1.2 Projectile Motion
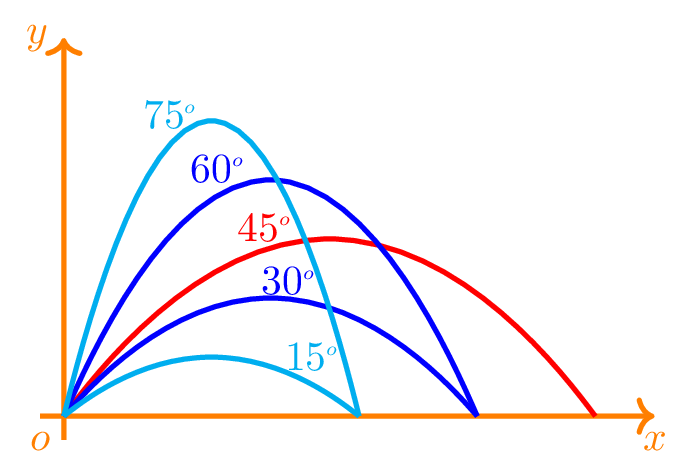
In normal day life, we encounter many examples where object moves along both horizontal and verticle direction together. Such type of motion is called projectile motion and the object moving in projectile motion is called a projectile. Hence, projectile is an object which has both horizontal as well as vertical motion. The path taken by the projectile is parabolic in nature [Figure 2.1.3]. We are not dealing with mathematical operation related to projectile motion here but we try to understand the projectile motion by the following figure. Since gravity only acts on the verticle direction the horizontal velocity remains constant always in projectile motion.
