Subsection 7.2.2 Binding Energy
Binding energy is the amount of energy required to separate a nucleons into the protons and neutrons. In an atomic nucleus, the protons and neutrons are held together by the strong nuclear force, which acts over short distances. The binding energy of a nucleus can be calculated by subtracting the total mass of its individual protons and neutrons from the total mass of the nucleus itself. According to Einstein’s famous equation,
\begin{equation}
E=mc^2,\tag{7.2.3}
\end{equation}
the mass difference between the two states is equivalent to the binding energy. The binding energy of a nucleus has important implications for both the stability of the nucleus and for the energy released during nuclear reactions. Nuclei with higher binding energy are generally more stable and less likely to undergo spontaneous decay, while nuclei with lower binding energy are more likely to undergo radioactive decay. Additionally, the energy released during nuclear reactions is directly proportional to the binding energy of the nucleus. When a nucleus is formed, protons and neutrons come together and bind to form the nucleus. This process is driven by the strong nuclear force, which acts over short distances to hold the particles together. The formation of a nucleus also leads to the release of energy. This energy is in the form of electromagnetic radiation and called the binding energy. It is the same amount of energy required to separate the protons and neutrons in the nucleus when broken down to individual components. For example: The deuterium (\({}_{1}^{2}H\)) has one proton and one neutron in its nucleus. So when they break apart we expect the mass of deuterium atom equals the mass of one proton (i.e. \({}_{1}^{1}H\)) and the mass of one neutron. Mass of one \({}_{1}^{1}H = 1.0078 u \) and mass of one neutron = 1.0087 u. Therefore the total mass of
\begin{equation*}
{}_{1}^{2}H = 1.0078 u+1.0087 u= 2.0165u\text{.}
\end{equation*}
The measured mass of \({}_{1}^{2}H\) however, is only \(2.0141 u,\) which is \(0.0024 u\) less than the combined mass of proton and neutron. This loss of mass (also known as mass defect) appears in the form of binding energy of the deuterium atom. Similarly when one deuterium nucleus combines with one tritium nucleus to form helium nucleus tremendous amount of energy released which was a binding energy. For example:
\begin{equation*}
{}_{1}^{2}H + {}_{1}^{3}H \longrightarrow {}_{2}^{4}He + {}_{0}^{1}n +\text{energy}\text{.}
\end{equation*}
Hence, the mass defect in this case is given by: total mass of \({}_{1}^{2}H + {}_{1}^{3}H = 2.0141\,u+3.0161 \,u= 5.0302\,u\) and total mass of \({}_{2}^{4}He + {}_{0}^{1}n = 4.0026\,u+1.0087\, u= 5.0113\,u\text{.}\) Hence the difference in these masses is a mass defect, \(m = 0.0189u\text{.}\) Note: Here \(u\) is the atomic mass unit. \(1 \,u = 1.67 \times 10^{-27} \,kg\text{.}\) This is the approximate mass of the hydrogen atom. Atomic mass unit is also caled Dalton. we can also consider \(1 \,u \) as \(1 gram/mole.\) 1 mole of anything is equal to \(6.022\times 10^{23}.\) Now,
\begin{align*}
\text{1 mole of H-1 atom} \amp = 1.0078 \,gram\\
or,\quad \text{mass of} \quad 6.022\times 10^{23} \quad \text{H-1 atom} \amp = 1.0078 \, gram\\
\therefore \quad \text{mass of 1 H-1 atom} \amp = \frac{1.0078 \quad gram}{6.022\times 10^{23}}\\
\amp =1.67 \times 10^{-24} \,gram = 1.67 \times 10^{-27} \,kg.
\end{align*}
This mass defect appears in the form of binding energy which can be calculated by equation (7.2.3)
\begin{equation*}
E = mc^2 = 0.0189\,u\times (3.0\times 10^8 \,m/s)^2
\end{equation*}
2
\(c=3.0\times 10^8 \,m/s\text{,}\) the velocity of light.
\begin{equation*}
E =0.0189\times 1.67 \times 10^{-27} \,kg\times (3.0\times 10^8 \,m/s)^2 = 2.84\times10^{-12} \,J
\end{equation*}
Hence, energy released from this reaction is \(1.78\times 10^7 \,eV\) or, 17.8 MeV.
3
\(1\,eV=1.6\times 10^{-19}\,J\) and \(1u = 931\, MeV\text{.}\)
Subsubsection 7.2.2.1 Binding Energy per Nucleon
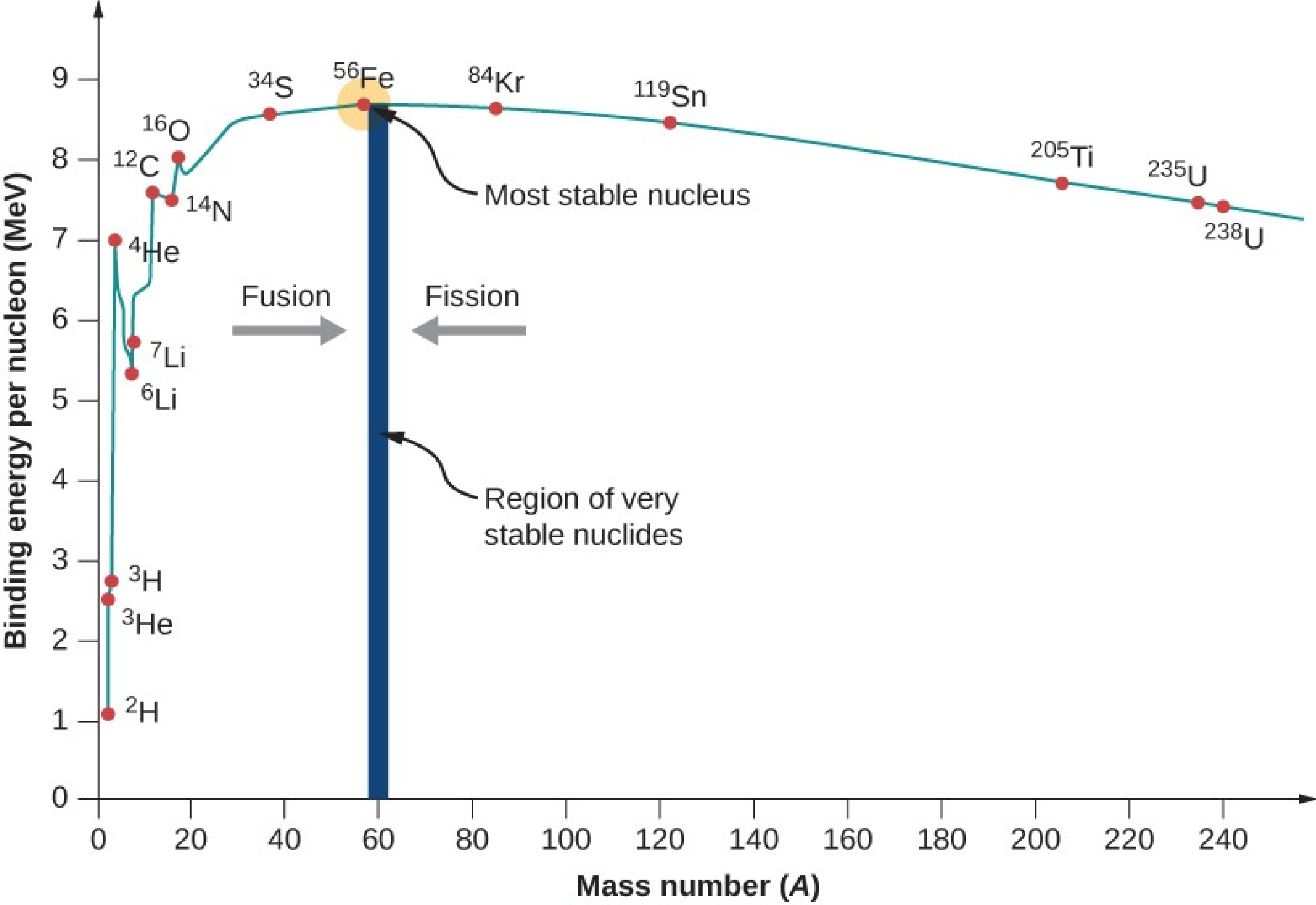
4
www.w3schools.blog/binding-energy-per-nucleonThe binding energy of a nucleus determines its stability against disintegration. The larger the binding energy, the more stable is the nucleus and vice a versa. The binding energy per nucleon, BE/A is the ratio of Binding energy of the nucleus to the total number of nucleons. It is found that the binding energy per nucleon varies from element to element. A graph Figure 7.2.4 is plotted with the mass number A of the nucleus along the X-axis and binding energy per nucleon along the Y-axis. The binding energy per nucleon increases sharply with mass number A upto 20. It increases slowly after \(A = 20\text{.}\) The curve becomes almost flat for mass number between 40 and 120. Beyond 120, it decreases slowly as A increases. The binding energy per nucleon reaches a maximum at A=56, corresponding to the iron nucleus (\({}_{26}^{56}Fe\)). Hence, iron has the most stable nucleus. At the lower end of the curve, smaller nuclei have relatively lower binding energy per nucleon compared to larger nuclei. This is because the attractive strong nuclear force, which holds the nucleons together, decreases rapidly with increasing distance between the nucleons. As a result, small nuclei tend to be less stable and more likely to undergo nuclear reactions, such as beta decay. At the higher end of the curve, larger nuclei have relatively lower binding energy per nucleon compared to smaller nuclei. This is because the repulsive electromagnetic force between the positively charged protons in the nucleus increases with increasing number of protons. This repulsive force limits the size of the nucleus and causes it to become less stable.
