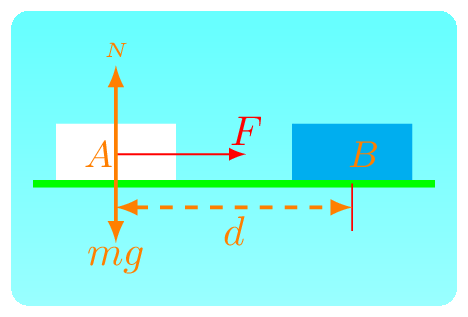
Work: an object is displaced along the same direction as of the applied force then work is said to be done by the force. In the
Figure 3.1.1 force
\(F\) is pushing a block of mass
\(m\) along its direction for a distance of
\(d\text{,}\) then work done,
\(W\) by this force can be calculated by
\begin{equation}
W = F d\tag{3.1.1}
\end{equation}
Work is a scalar quantity as it is a measure of transfer of energy from one object to another. The SI unit of work is Joule\(=N\cdot m\text{.}\) In FPS system, \(ft.lb = foot.pound\text{,}\) and in CGS system, \(erg =dyne.cm\) are the work units.
In
Figure 3.1.1 force
\(F\) is along the direction of horizontal and the block is also displaced along the same direction from point A to point B. In this case work done by the force is given by multiplication of force
\(F\) and the displacement
\(d\text{.}\) In this figure work done by the weight
\(mg\) and normal force
\(N\) is zero as these forces are perpendicular to the displacement
\(d\text{.}\) However, if slanted force
\(F\) is involved in doing work, then the work is not zero but can be determined by the projected force which is not in the scope of this book.
Remember for work to be done, foce and displacemenet must be non-zero. Work may be positive, negative, and zero. For example: work done by applied force along the direction of displacement is positive, work done by the frictional force is negative, and work done by the force perpendicular to the displacement is zero.
Energy: The capacity of doing work by a force is called an energy. It is also a scalar quantity and has the same unit as work. There are many forms of energy, but they all fall into two categories: potential energy and kinetic energy. These energies are also called a mechanical energy. Potential energy is the energy of position of the object. It is also a stored energy on the object which is equal to the work done on the object to bring it to this position. There are several forms of potential energy, including: gravitational potential energy, chemical energy, elastic energy, nuclear energy, sound energy, heat energy, light energy, geothermal energy, etc. Chemical energy: It is energy stored in the bonds of atoms and molecules. It is the energy that holds these particles together. Foods, biomass, petroleum, and natural gas are some examples of stored chemical energy. During photosynthesis, sunlight gives plants the energy they need to build complex chemical compounds. When these compounds are later broken down, the stored chemical energy is released as heat, light, motion, and sound. Elastic energy: It is an energy stored in objects by the application of a restoring force. Compressed springs and stretched rubber bands are examples of elastic energy. Nuclear energy: It is an energy stored in the nucleus of an atom that binds the nucleus together. The energy can be released when the nuclei are combined or split apart. Nuclear power plants split the nuclei of uranium atoms in a process called fission reaction . The sun combines the nuclei of hydrogen atoms into helium atoms in a process called fusion reaction . In both the fission and fusion reactions, mass is converted into energy, according to Einstein’s mass-energy
\begin{equation}
E = mc^2\tag{3.1.2}
\end{equation}
principle. Gravitational potential energy: or Potential energy: It is the energy of position or place. It is the work done in lifting an object against gravity near the earth’s surface. Gravitational Potential energy depends only on the distance from the ground, not on the object’s motion. It is given by
\begin{equation}
PE = Fd=mgh\tag{3.1.3}
\end{equation}
Here \(F\) is the weight of the object \(mg\) and distance \(d\) is the height \(h\) at which the object is lifted. A rock resting at the top of a hill contains gravitational potential energy because of its position. In hydropower dam, water in the reservoir stored a gravitational potential energy. Kinetic energy: It is the energy of a body due to its motion. If a body of mass \(m\) is moving with a velocity \(v\) then kinetic energy is given by,
\begin{equation}
KE = \frac{1}{2}mv^2\text{.}\tag{3.1.4}
\end{equation}