Subsection 2.2.5 Newton’s Law of Gravitation
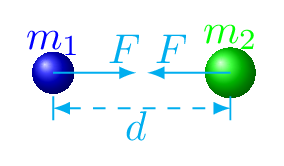
Newton observed that when an object falls it was accelerated toward the earth. Since the cause of such acceleration is an unbalanced force, there must be a force pulling that object toward the earth. On this basis, he came up with an idea called Newton’s Law of Universal Gravitation. It states that any two masses in the universe attract each other with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance between them [Figure 2.2.4]. Mathematically,
\begin{equation}
F = G\frac{m_1\times m_2}{d^2}\tag{2.2.7}
\end{equation}
here, \(G=6.67\times 10^{-11} \,Nm^2/kg^2\) is an universal gravitational constant, \(m_1\) and \(m_2\) are the masses of two objects, and \(d\) is the distance between the them.
Subsubsection 2.2.5.1 Escape Velocity
Escape Velocity is the minimum velocity required by an object at which if it can be thrown out of the planet then it never fall back on the planet again. If a stone of mass m is thrown out from the earth with an escape velocity \(v_e\) then it never fall back on the earth again. The escape velocity depends on the mass and radius of the massive body and is given by the formula:
\begin{equation}
v = \sqrt{\frac{2GM}{r}}\tag{2.2.8}
\end{equation}
Here, \(G\) is universal gravitational constant, \(M\) is the mass of the planet, and \(r\) is the radius of that planet. The escape velocity of earth is 11.2 km/s.
