Chapter 2 Motion
If an object is changing its position with time then the object is said to be in motion. It is a relative quantity. For example, suppose Aron and Bob are sitting in car then they are at rest relative to each other even if the car is running on the road or just at rest in a parking lot. However, if Charley is observing Aron and Bob from outside of car and car is moving then both of them are in motion for Charley and same applies to Arron and Bob for Charley. Meaning Aron and Bob can tell Charley is in motion going behind them but they are at rest. It is our human instict that Aron and Bob understand that they are going in the car, so they are in motion with with respect to the road and Charley is at rest. Here we are going to learn motion of objects with respect to the earth.
Motion can be described in terms of distance, displacement, position, time, speed, velocity, and acceleration. Motion is an act of movement. There are different types of motion we come accross in our daily life. They are linear motion, circular motion, periodic motion, harmonic motion, vibrational motion, uniform motion, non-uniform motion, etc. To understand the motion, we need to learn physical quantities and their types.
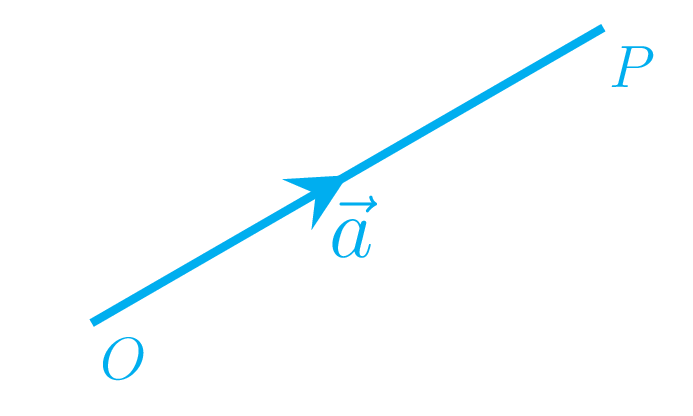
The concept of physical quantity has already been introduced in Section 1.3. Here we are going to learn little more about physical quantity . As we know anything that can be measured in numbers and units are called a physical quantity. Physical quantities are of two types, namely “scalar physical quantity” (or scalars) and “vector physical quantity” (or vectors). Scalars has magnitude only and no direction is involved in this physical quantity. For example: distance, speed, mass, time, density, temperature, currency, work, energy, current, power, pressure, etc. Vectors has both magnitude and direction. For example: displacement, velocity, acceleration, force, weight, momentum, torque, etc. Vector quantity is represented by an arrow pointing along its direction and size of the arrow represents its magnitude. In Figure 2.0.1 \(\vec{a}\) is a vector OP which is pointing along its direction and the size of arrow is representing the magnitude of that vector. Actually, it is not logical to scale the vectors everytime we draw them on the paper, hence we distinguish the vectors just by their magnitude value and direction but not by the size of the drawing.